Vejgeometri

Jeg fik engang foræret en gammel brugt udgave af den legendariske bog Lærebog i matematisk analyse af Bohr og Mollerup. Bogen blev brugt af flere generationer på Danmarks Tekniske Højskole (nu Danmarks Tekniske Universitet, DTU), og vist også på Københavns Universitet. I begyndelsen af 2004 fandt jeg lidt tilfældigt en gammel gulnet avisartikel, som var skubbet ind mellem nogle sider i bogen. Der var tale om en artikel fra 1962 fra Ingeniørens Ugeblad: Smukkere og bedre veje ved hjælp af klotoider. Det viste sig at være en højst interessant artikel om en smuk anvendelse af matematik i forbindelse med vejprojektering. Jeg henvendte mig siden til DTU og blev henvist til en pensioneret lærer i vejbygning. Han kunne anvise nogle bøger, hvor jeg kunne læse om teorien om de såkaldte klotoider. Det viste sig, at der var langt mere matematik i vejbygning end jeg anede: Horisontalkurver, kørselsdynamik, sidehældning, friktion, vertikalkurver etc. En god blanding af matematik og fysik! I mine videre undersøgelser viste det sig, at de såkaldte klotoider også blev anvendt i optik, til anlæg af togspor, skihopbaner og meget eksotisk ved konstruktionen af rutschebaner i forlystelseshaver. Jeg vil komme ind på sidstnævnte nedenfor. Klotoider har endda været foreslået som banekomponenter i forbindelse med minedrift.

  1. Matematikken bag klotoiden
  2. Klotoiden anvendt i vejbygning
  3. Æstetikkens betydning
  4. Besøg på amtets vejafdeling
  5. Klotoider og rutsjebaner
  6. Note og tillæg
  7. Hjemmesider
  8. Litteratur

 

Matematikken bag klotoiden

En klotoide eller Cornu Spiral er en matematisk defineret kurve, som har følgende parameterfremstilling:

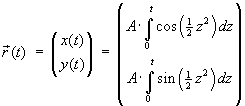
A kaldes for klotoide-parameteren. Koordinatfunktionerne er altså integraler, og disse integraler dukker faktisk også op indenfor optik igennem de såkaldte Fresnel-integraler. Banekurven ser således ud:

 

 

Klotoiden anvendt i vejbygning

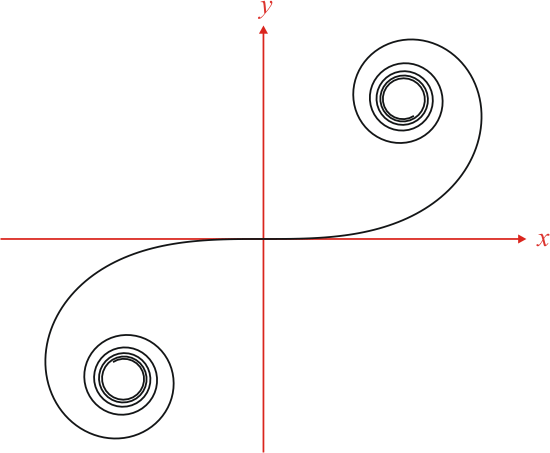
Klotoidens vigtigste egenskab er, at hvis man kører i kurven med konstant fart, så vil krumningen af kurven være proportional med tiden. Det betyder, at hvis man kører i kurven med konstant fart, så skal man dreje rattet med konstant vinkelhastighed for at holde sig i kurven. Dermed kan klotoiden benyttes som bindeled mellem vejstykker bestående af rette linjestykker og cirkelbuer. Det er derfor klotoiden omtales som en overgangskurve. Hvis man lod en cirkelbue forløbe direkte over i dens tangent i buens endepunkt, ville man gå fra en kurve med krumning 1/R, hvor R er radius i cirklen, direkte over i en linje, der har krumning 0. Der vil med andre ord være en diskontinuitet i krumningen - altså et pludseligt spring i krumning, som vil betyde, at rattet skal drejes en bestemt vinkel momentant. Hvis radius i cirkelbuen er stor betyder dette ikke så meget, da der er plads i vejbanen til at korrigere. Ubehaget vil øges, hvis radius mindskes. Ved at skyde en overgangskurve ind i form af en klotoide vil krumningen gradvist ændres fra 1/R til 0, således at man får en kurve, hvor såvel den første afledede og den anden afledede er kontinuerte, hvilket igen medfører, at krumningen bliver kontinuert. Resultatet er en pæn harmonisk kurve. Situationen er illustreret på figuren nedenfor: Det rette linjestykke befinder sig på den negative del af x-aksen. I origo går den over i klotoiden, der strækker sig fra O til P. I punktet P fortsætter klotoiden over i cirklen. Cirklen skal naturligvis være krumningscirkel til klotoiden i endepunktet P.

 

Æstetikkens betydning

En anden fordel ved klotoiden er, at den får vejen til at få et bedre æstetisk forløb, når chaufføren i køretøjet ser det perspektiviske billede af vejen foran sig. Jeg har udregnet det perspektiviske billede i tilfældet med en helt vandret vej. På det første billede nedenfor går det lige stykke direkte over i cirkelbuen (dårlig løsning), på det næste er der indskudt et stykke klotoide imellem linjestykket og cirkelbuen (gode løsning). Øjenhøjden er 1,5 meter, klotoideparameteren er 200 meter og cirklens radius er 300 meter. Billedplan vinkelret på køreretning.

 

 

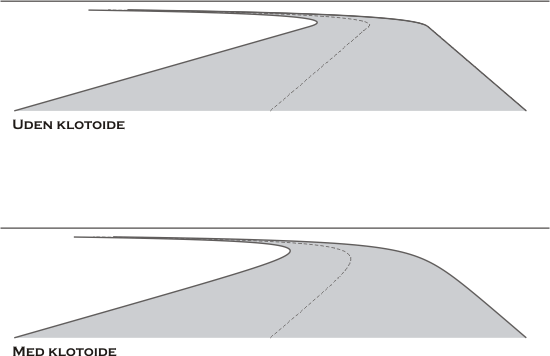
Man ser, at det på det perspektiviske billede uden klotoide ser ud til, at der er et mindre knæk i kurven. Det perspektiviske billede med klotoide giver derimod et bedre og mere korrekt indtryk af den kurve, man kører ind i. Æstetiske hensyn er i høj grad noget man interesserer sig for, dels fordi man ønsker føreren en så god "køre-oplevelse" som muligt, dels af sikkerhedsmæssige årsager. Det har for eksempel vist sig, at ved brug af lange lige strækninger bliver føreren lettere lullet i søvn på grund af de ensformige køre-oplevelser, med flere uheld til følge.

 

Besøg på amtets vejafdeling

For at få et bedre helhedsindtryk af hvordan vejprojekteringsafdelingerne i Danmark arbejder, og for at se om man virkeligt gør brug af de i lærebøgerne beskrevne klotoider, henvendte jeg mig til vejafdelingen for Sønderjyllands Amt, der befinder sig på amtsgården iAabenraa. Her tilbød en venlig ingeniør at jeg kunne besøge afdelingen. Det endte med, at jeg fik en grundig rundvisning i vejprojektering i et par timer på amtsgården. En stor tak til afdelingen for deres venlighed!

På amtsgården kunne jeg se en opslagstavle med gamle linealer, cirkel- og klotoide-skabeloner, som blev anvendt intensivt før computerens tidsalder. Du kan se et par eksempler på klotoide-skabeloner herunder.


Men som bekendt: Computerens tidsalder har ændret meget. Nu anvender man dedikeret software, for eksempel programmet Novapoint sammen med det store tegneprogram AutoCAD. Novapoint er beregningsdelen, som for eksempel kan beregne klotoide-delen, som passer imellem et ret linjestykke og en cirkelbue.

Billedet nedenfor er et udsnit af et screendump, som viser, hvordan Novapoint og AutoCAD arbejder sammen. Ovenpå et kort fra Kort og Matrikelstyrelsen kan man lægge linjeføringen og studere hvordan det kommer til at tage sig ud. På figuren forestiller den grønne kurve et linjestykke, den blå kurve en klotoide og den røde kurve en cirkelbue. Man kan også aflæse/indtaste radier, klotoideparametre etc...

Klik på billedet for at se et større udsnit af billedet!!

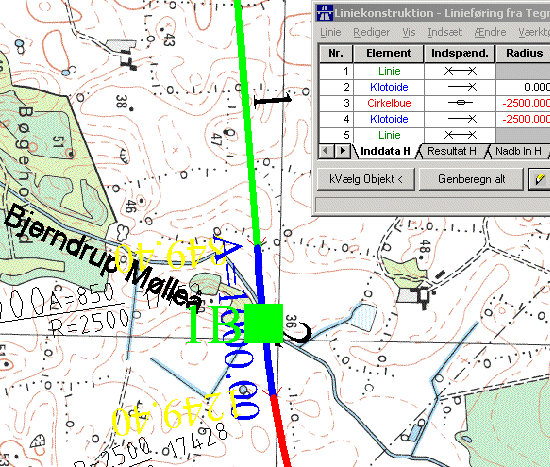
(Vist med tilladelse fra Kort- og Matrikelstyrelsen).

Meget aktuelt kunne vejafdelingens ingeniør vise mig skitseprojekteringen af et motorvejsstykke mellem Kliplev og Sønderborg, som kun fremtiden kan vise om bliver vedtaget.Den ingeniør-mæssige planlægning af en sådan motorvej er en lang proces. Man udarbejder normalt nogle få forslag til linjeføring. Du kan studere det prioriterede løsningsforslag, den såkaldte I-løsning på Sønderjyllands Amts hjemmeside: www.vejetilals.sja.dk. Her er der en masse information og diverse visualiseringer.

Ved valg af linjeføringen må man tage hensyn til en lang række forhold: Formål med vejen, økonomi, landskab, trafiksikkerhed, fredningshensyn, kørselsdynamik, æstetik, afvekslende landskabsoplevelser etc...

Ved opmålinger på landjorden ved hjælp af en såkaldttotalstation eller GPS kan man få et netaf paspunkter (x,y,z). Sammenholdes disse med luftfotos taget ved overflyvninger eller alternativt såkaldte laserscanninger, kan man ved hjælp af programmel såsom Novapoint danne en trådmodel eller gittermodel af typografien. Dermed har man oplysninger om landskabets 3D-forhold. Hvis man ønsker koordinaterne for et punkt, som ikke er et gitterpunkt, så kan disse bestemmes ved interpolation udfra koordinaterne i de nærmeste gitterpunkter - man kan sige, at gitterpunkterne giver en triangulering af landskabet.

Man kan for eksempel lægge et tænkt vejstykke ind i modellen og se, hvordan det tager sig ud. For at kunne vurdere om vejens tracé er i orden har vejafdelingen i Aabenraa udarbejdet animationer, der viser, hvordan en biltur vil tage sig ud, når man kører ud af de forskellige løsningsforslag. Jeg har fået et par screendumps fra animationerne. Billede nummer 2 nedenfor viser motorvejens passage mellem dødisbakken Lindebjerg og Kidding Tykke.

 

(Luftfotos, som ligger til grund for animationen er udført af COWI. Firmaet har givet mig tilladelse til at bringe billederne. Den efterfølgende animation er udført af firmaet Cadpeople ApS).

Når man er nået meget langt i processen med at rette vejen til og finde ud af, hvor der skal fjernes jord eller tilføjes jord for at vejen får et fint forløb, plejer man at gå ud i landskabet for få et sidste indtryk. En vejs rumlige forløb, som involverer vejens linjeføring og længdeprofil betegnes vejens tracé. Ved at gå en tur i landskabet med en mappe fuld af perspektiviske billeder (af typen vist nedenfor) vil en erfaren traceringsekspert være i stand til at opdage problemer, som man kan nå at rette før det endelige vejforslag er færdigudviklet. Der kan også være nogle objekter i landskabet, som ikke var taget med i modellen, men som kan have betydning. Det gælder nemlig om at få vejen til at få en indre og ydre harmoni. Den indre harmoni, som beskrives ved vejens rumlige geometri og den ydre harmoni, som omhandler vejens indpasning i omgivelserne. Broer, beplantning og udstyr har også betydning for helhedsindtrykket!

Klik på billedet for at se et større udsnit af billedet!!

Jeg vil afslutte min omtale af vejprojektering her, velvidende at der er mange flere områder som kunne være omtalt, herunder blandt andet kørselsdynamik.

 

Klotoider og rutsjebaner

Som nævnt i indledningen til denne side er en anden vigtig anvendelse af klotoider i forbindelse med udformningen af rutsjebaner i forlystelsesparker. Mennesket har som bekendt altid prøvet at udforske sine muligheder til det yderste, og indenfor kunsten at kunne konstruere den rutsjebane, som kan give det største gys, lever dette princip i bedste velgående. I USA er der således i dag stor konkurrence blandt "Amusements Parks" om at eje den mest uhyggelige rutsjebane. Passagererne bliver slynget rundt i kurver og loops under stor G-påvirkning og oplever det ene øjeblik vægtløshed, det andet øjeblik presses de kraftigt tilbage i sædet.

En af de store indenfor forlystelsespark-industrien har været tyskeren Anton Schwarzkopf, som sammen med sin uundværlige chefingeniør Werner Stengel var den nyskabende i forlystelses industrien. Det startede for alvor i 1960'erne og forløb helt frem til 1995, hvor Anton Schwarzkopf gik på pension. Werner Stengel er kendt som "Rutsjebanernes mester". Han konstruerede blandt andet verdens første succesfulde vertikal-loop. Man havde længe forinden forsøgt at konstruere brugbare cirkulære loops, men var stødt på det problem, at passagererne blev udsat for voldsomme G-påvirkninger, som undertiden medførte alvorlige personskader. Werner Stengel fandt en genial løsning på problemet, idet han forslog at anvende stykker af klotoider i loopet. Dette skridt reducerede G-påvirkningerne betydeligt. Lad mig prøve at forklare problematikken i det følgende:

Når et objekt bevæger sig rundt i en kurve, bliver objektet udsat for en acceleration, såfremt det skifter retning og/eller hvis dets fart ændres. Lad os indføre nogle størrelser:

Man kan vise, at accelerationen kan opløses på følgende måde efter retningerne bestemt af den normerede tangentvektor og den normerede normalvektor:

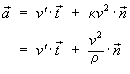
hvor vi har udnyttet, at krumningsradius er omvendt proportional med krumningen. Situationen kan illustreres på følgende måde:

 

 

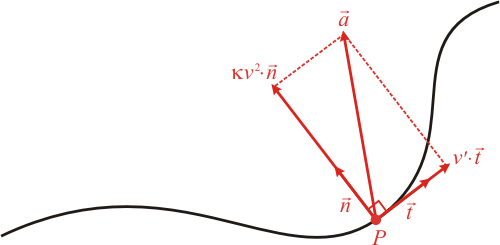
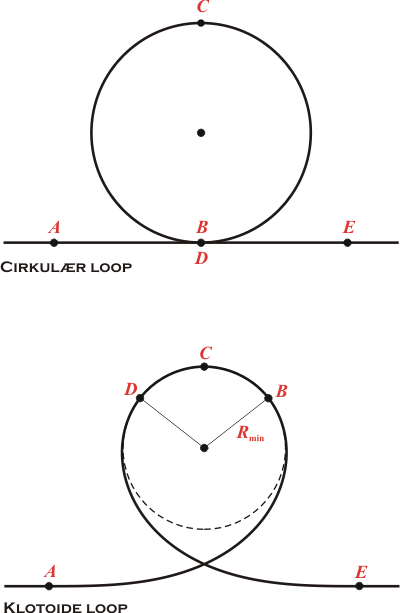
Accelerations-komponenten i normalens retning er særligt interessant. Bemærk, at den er den samme som den man udsættes for i en jævn cirkelbevægelse - naturligvis! Inden man kører ind i et loop skal man have en vis fart på, således, at man kan nå rundt i loopet. Vognen vil altså typisk have en ret stor fart i bunden og farten vil så aftage opefter i takt med, at den potentielle energi øges. Hvis man benytter et cirkulært loop, som vist på figuren nedenfor, så vil krumningsradius altså altid være lig med radius i cirklen, men da farten i B er noget større end farten i C, så vil accelerationen i normalens retning altså være meget større i B. Problemet med de store G-påvirkninger opleves altså især i bunden af loopet! Werner Stengel indså, at hvis man øger krumningsradius i bunden, så vil man få mindsket accelerationen. Dette fremgår direkte af ovenstående formel! Klotoiden har netop stor krumningsradius i starten, og kurven har ydermere den fordel, at krumningen øges lineært med den tilbagelagte strækning i loopet. Situationen kan ses på figuren med Klotoide-loopet: Et stykke oppe af loopet (i punkt B) lader man klotoiden gå over i dens krumningscirkel i B. Dette sikrer, at krumningen bliver kontinuert, dvs. den fulde kurve er kontinuert differentiabel af 2. orden! Werner Stengel var i stand til at reducere G-påvirkningen fra ca. 10G til ca. 4,5G. Lidt længere nede kan du se billederne af to klotoide-loops.

 

 

 

(With permission from Michael Pentenburg, www.pantenburg.com)
Billedet viser rutsjebanen Looping Star fra Bobbejaanland i Belgien.
Rutsjebanen, som har et klotoide loop, blev i 2003 udskiftet med en ny!

 

(With permission from Joel A. Rogers, www.coastergallery.com)
Viser et dobbelt klotoide-loop i rutsjebanen Shockwave i forlystelsesparken Six Flags over Texas, Arlington, Texas. Den er bygget af Schwarzkopf og taget i brug i 1978. Tophastighed: 96,5 km/t.

 

Note og tillæg

Jeg har lavet en større note (42 sider) om emnet Vejgeometri. Noten indeholder også lidt om klotoidens anvendelse i forbindelse med rutsjebaner! Blandt andet G-påvirkninger i loops! Noten kan måske benyttes under det valgfrie forløb i 3g matematik. For hjælp til at downloade klik her. For information om pdf format og brug af Adobe Reader klik her.

For læsere, som ønsker et mere teknisk kendskab til begrebet g-påvirkning og relativ bevægelse i rummet, kan følgende tillæg måske være en hjælp:

  

Forsøg med g-påvirkning

Man kan udføre forsøg med accelerationer i forlystelser ved hjælp af forskellig fysikudstyr, fx i Tivoli i København, og forsøge at udregne eksperimentelle værdier for g-påvirkningerne ud fra det. Man skal dog være opmærksom på, at det er ret kompliceret at bestemme g-påvirkninger, hvis man foretager bevægelser i for eksempel et loop. Her vil der være tale om et ledsagende koordinatsystem, som ændrer retning: Sensorens koordinatsystem er anderledes end laboratoriets koordinatsystem, som er "fast" i forhold til jorden. For at beregne g-påvirkningen kræves altså viden om det ledsagende koordinatsystems drejning i forhold til det faste "jordsystem". Det har man normalt ikke. Når det gælder g-påvirkninger anbefales det for gymnasieelever derfor kun at udføre forsøg i forlystelser, som foretager bevægelser i meget velbestemte retninger, fx op og ned! Hvis du klikker på billedet nedenfor kan du se en video om, hvordan det kan gøres i Wireless Dynamic Sensor System (WDSS), som er udstyr fra firmaet Vernier.
 


Tivoli har imidertid selv offentliggjort grafer for de eksperimentelle værdier af g-påvirkningen i et par forlystelser:

Det gyldne tårn i Tivoli

Dæmonen i Tivoli

Derudover er der naturligvis også mange andre muligheder for at studere teoretiske og eksperimentelle resultater i andre forlystelser ...

 

Hjemmesider

Sønderborgmotorvejen  (Motorvejen Kliplev-Sønderborg)
www.coastergallery.com (Stort galleri over amerikanske rutsjebaner).
schwarzkopf.coaster.net
www.rcdb.com (Meget omfattende database over rutsjebaner (Rollercoasters).
www.rcstengel.com (Werner Stengels Ingeniør Bureau).
http://www.emu.dk/modul/rutschebanefysik (En fin side om rutsjebanefysik på EMU).

 

Siden er opdateret 31.12.18.

 

Litteratur

  1. Jørgen Dejgaard & Claus Michelsen. Trafikmodeller. Matematikkens aspekter fra Matematiklærerforeningen, 2001. (Bogen kan bruges til at studere andre sider af matematik i forbindelse med veje og trafik).
  2. Fr. Fabricius-Bjerre. Lærebog i geometri II. Differentialgeometri og kinematisk geometri. 6. udgave, 1. oplag. Polyteknisk forlag, 1977.
  3. Dr.-Ing. E. H. Hans Lorenz. Trassierung und Gestaltung von Strassen und Autobahnen. Bauverlag GMBH.
  4. Mogens Nørgaard Olesen. Plane kurver. Systime, 1984.
  5. Bent Thagesen (redaktør). Lærebog i vejbygning. Bind I. Trafik og geometri. Polyteknisk forlag, 1991.
  6. Bent Thagesen (redaktør). Veje og stier. Polyteknisk forlag, 1. udgave, 2. oplag, 2000.