Tutorial 3
Terning i frontperspektiv
I denne øvelse skal du studere en terning i frontperspektiv,
herunder være opmærksom på perspektiviske forkortninger.
Vi skal også se på forsvindingspunkter! Vi vil i hele øvelsen anvende
lodret billedplan.
- Aktiver feltet Top og marker huset og slet det med
Delete-tasten.
- Vælg Box Tool i værktøjslinjen (ikke Rectangle Tool!!) og træk først et rektangel
ud i feltet Top. Husk at efter du har trukket kvadratet
ud, er du ikke færdig! Når du flytter cursoren lidt op eller ned, så vil den tredje dimension blive dannet, hvilket kan ses i de øvrige felter. Når du er tilfreds med højden (egentligt ligegyldig her), venstreklikker du.
- Din kasse er sandsynligvis ikke en terning, så vi skal have
den redigeret via de absolutte data på den grå bjælke forneden. Vælg først View
> Rulers (Ctrl+R) for at få vist linealer. Det
skal hjælpe os i det følgende. Klik på Pick Tool i værktøjslinjen
og marker kassen.
- Sørg for at kassen får dimensionerne 10x10x10 meter via Size og at dets midtpunkt kommer til at ligge i punktet med koordinaterne
(0,-5,5), underforstået i meter, via Position. Husk, at hver gang du ændrer
et tal i et felt, skal du afslutte med at bruge Return-tasten
eller klikke på Apply!!!
Nu skulle det gerne se således ud:
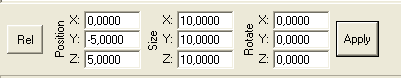
Bemærk,
at terningen nu fint står på jorden i højden 0! Terningen kunne også være lavet direkte ved brug af Snap-To-Grid funktionen, dvs. ved at holde Shift-tasten nede samtidigt med at kassen trækkes ud. Hvis man endda samtidigt holder Ctrl-tasten nede, så vil kassen endda blive tvunget til at have kubiske mål ...
- Vi skal nu ændre øjepunktets placering og synsretningen.
Du kan selvfølgelig gøre det interaktivt ved at trække i synspilen.
Du kan imidlertid også gøre det helt præcist via Edit Perspective
dialog boksen. Den kan fås frem via View > Edit Perspective
eller lettere: ved at vælge Edit Perspective knappen,
forestillende et øje,
direkte fra værktøjslinjen. Du kan herefter ændre Eye Point
til (0,20,5) og Viewing Direction til (0,-10,0), som vist
på figuren nedenfor. Du kan se den umiddelbare virkning uden
at dialogboksen lukkes, hvis du klikker på Apply. Hvis
du klikker op OK vil boksen desuden blive lukket.
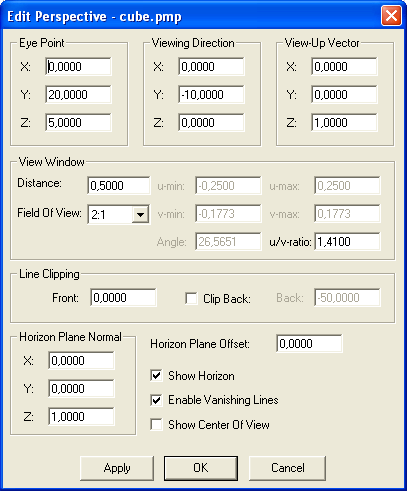
Du
skulle nu gerne have følgende felter:
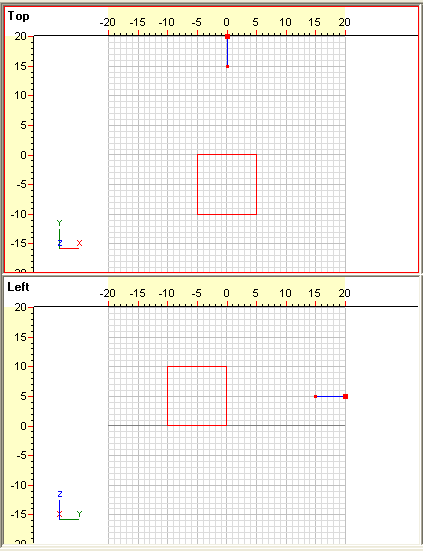
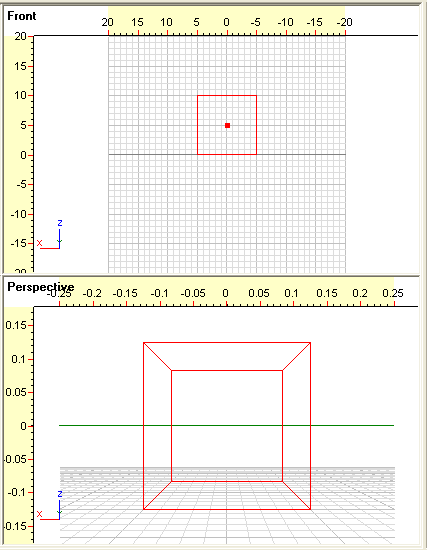
- Med valget af synsretning under punkt 5 har vi lodret
billedplan fordi Z-koordinaten i synsretningen er 0. Endvidere
har vi at gøre med et front-perspektiv, da billedplanen,
som er vinkelret på synsretningen, er parallel med frontsiden
på terningen. Terningen har 12 kanter. Heraf er 4 kanter, linjer,
som forløber " ind i dyben" (dybdelinjer). De
har derfor hver et forsvindingspunkt. Da disse 4 kanter
er parallelle med synsretningen vil deres forsvindingspunkt
være sammenfaldende med hovedpunktet, som ligger på
horisontlinjen. Vi skal se, om det passer ved at få programmet
til at forlænge kanterne til deres respektive forsvindingspunkter.
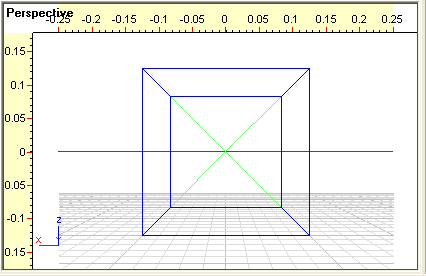
Marker en
af de fire dybdelinjer. Jeg vil anbefale dig at gøre det via
objekt-træet ude til højre. Når du klikker på en linje, vil
det med rødt blive vist hvilken linje, som er markeret - i alle
projektioner! Når en linje er markeret, vælg da Object >
Show Vanishing Lines (F5), så tegnes forlængelsen
til forsvindingspunktet! Gentag dette for de tre øvrige dybdelinjer.
Så skulle du gerne have følgende:
NB!
Hvis du markerer hele objektet og taster F5 vil alle linjer
i objektet blive forlænget til deres respektive forsvindingspunkter,
såfremt de findes!!!
- Gem filen med navnet tut3.pmp.
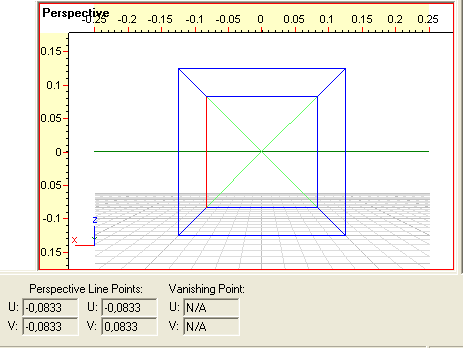
- Marker en af de to bagerste lodrette linjer i terningen
via Object Manager'en:

Bemærk,
at der i det store grå felt forneden bliver vist de perspektiviske
koordinater for linjens to endepunkter. Du kan eventuelt bruge
disse til at beregne perspektiviske forkortninger. Linjen
har ikke noget forsvindingspunkt, så der står N/A i felterne
for Vanishing Point.
- Prøv at bevæge øjepunktet væk fra kassen, ved via Edit
Perspective dialogboksen at ændre Y-koordinaten til øjepunktet
til et større tal, fx 40. Da vil du godt nok ikke længere kunne
se øjepunktet i felterne, da punktet ligger udenfor scenen.
Du kan dog fint se det perspektiviske billede alligevel:
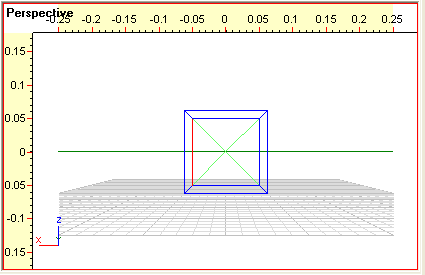
Hvad
er der sket med forholdet mellem de perspektiviske længder af
de forreste og de bagerste kanter i terningen, når du sammenligner
med tegningen under punkt 8? Prøv at drage nogle konklusioner
.....
NB! Hvis øjepunktet skulle ende udenfor scenen, så kan du bringe det tilbage igen ved at klikke på Reset Eye Point knappen i værktøjslinjen. Du kan selvfølgelig også gøre det via Edit Perspective dialogboksen!
- Måske ønsker du at have lidt mere plads på scenen,
så du blandt andet kan se synspilen. Så kan du for eksempel
vælge View > Scene Properties... og ændre værdierne
til: X-min = -40 X-max = 40 Y-min = -40 Y-max = 40 Z-min
= -40 Z-max = 40. Afslut med OK.
- Lad nu observatøren bevæge sig 10 meter til venstre,set fra dennes synspunkt, ved at
ændre øjepunktet til (10,40,5). Så fås følgende perspektiviske
billede:
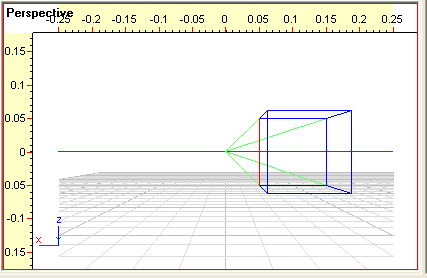
- Lad herefter observatøren bevæge sig 8 (meter) op ved at
ændre øjepunktet til (10,40,13). Så fås følgende perspektiviske
billede:
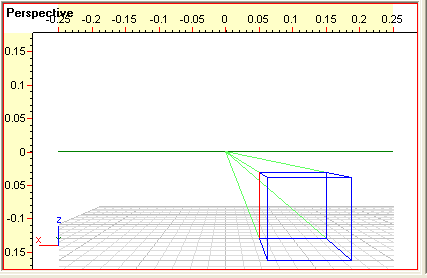
- Som du kan se på linealerne er billedets dimensioner 0,50m i længden og ca. 0,36m i højden. Mere nøjagtige dimensioner
kan du i øvrigt finde ved at klikke på knappen med øjet, som
viser Edit Perspective dialogboksen: Kig på værdierne
i felterne for u-min, v-min, u-max, v-min felterne, som er greyed
out. Billedet kan altså ikke være på et A4 papir, selv hvis
det ligger ned. Du kan selvfølgelig ved en udskrift vælge at
afmærke Fit to page, men du kan også vælge at styre det
selv ved at ændre distancen, dvs. afstanden til billedplanen.
Den er som default sat til 0,50m. Her kan du for eksempel foretage
en ændring af værdien for distancen til 0,28m. Dette vil blot
forårsage en skalering af den perspektiviske tegning,
dvs. en formindskning i dette tilfælde! På skærmen vil tegningen
ikke skifte størrelse, men du kan se, at linealerne ændrer værdier
..... :
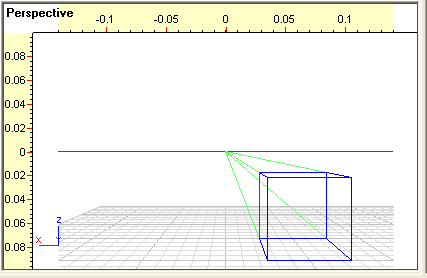
Herefter
kan tegningen være på et A4 ark!
- Gem filen.
|

